Remember the Lab we did way back when?
I'll just give a quick review of it.
Our object was to observe the reactions and determine the limiting and the excess reactants. Then find out the percent yield by comparing the actual mass with theoretical mass.
This lab took us two classes because we had to create precipitate solution and then filter the precipitate separate from the solution.
We had to calculate the masses of filter paper, dried filter paper with the precipitate and the dried precipitate.
There were few sources of error: Not having the exact required amounts of solution and the uncertainty of the centigram which we used to calculate the masses.
In conclusion, we proved that percent yield is true and that it wasn't 100% because not all reactants react completely because of the wrong conditions.
Sunday, April 10, 2011
Percent Purity
Fun break first!!

Many samples of chemicals are not pure. We can define percent purity as

Many samples of chemicals are not pure. We can define percent purity as
mass of pure compound in the impure sample x 100%
total mass of impure sample
If an impure sample of a chemical of known percent purity is used in a chemical reaction, the percent purity has to be used in stoichiometric calculations. Conversely, the percent purity of an impure sample of a chemical of unknown percent purity can be determined by reaction with a pure compound as in an acid-base titration. Percent purity can also be determined, in theory, by measuring the amount of product obtained from a reaction. This latter approach, however, assumes a 100% yield of the product.
Examples
3Mg(OH)2 + 2H3PO4 ----> Mg3(PO4)2 + 6H2O
(a) Calculate the mass of Mg3(PO4)2 that will be formed (assuming a 100% yield) from the reaction of 15.0 g of 92.5% Mg(OH)2 with an excess of H3PO4
mass Mg(OH)2 = 15.0 x 0.925 = 13.875 g
mass Mg3(PO4)2 =
13.875 g Mg(OH)2 x 1 mol Mg(OH)2 x 1 mol Mg3(PO4)2 x 262.9 g Mg3(PO4)2
58.3 g Mg(OH)2 3 mol Mg(OH)2 1 mol Mg3(PO4)2
= 20.9 g Mg3(PO4)2
(b) Calculate the mass of 88.5% Mg(OH)2 needed to make 127 g of Mg3(PO4)2, assuming a 100% yield.mass Mg(OH)2 =
127 g Mg3(PO4)2 x 1 mol Mg3(PO4)2 x 3 mol Mg(OH)2 x 58.3 g Mg(OH)2
262.9 g Mg3(PO4)2 1 mol Mg3(PO4)2 1 mol Mg(OH)2
= 84.49 g Mg(OH)2.
mass 88.5% Mg(OH)2 =
84.49 g Mg(OH)2 x 100 g 88.5% Mg(OH)2 = 95.5 g
88.5 g Mg(OH)2
(c) Calculate the percent purity of a sample of Mg(OH)2 if titration of 2.568 g of the sample required 38.45 mL of 0.6695 M H3PO4.
mass Mg(OH)2 =
38.45 mL H3PO4 x 0.6695 mole H3PO4 x 3 moles Mg(OH)2
1000 mL H3PO4 2 moles H3PO4
x 58.3 g Mg(OH)2
1 mole Mg(OH)2
= 2.251 g Mg(OH)2
Percent Purity = 2.251 x 100% = 87.7%
2.568
Wednesday, April 6, 2011
Percent Yield
Why there is a percent yield...
Reactions rarely produce the predicted amount of product from the masses of reactants in the reaction .An example of this is the reaction of carbon with oxygen. Normally we expect a 1 mol yield of carbon dioxide for every mol of carbon burned. This does not always happen.
C(s) + O2(g) --- > CO2(g)
If you burn 12 grams of carbon to make CO2, then amount of carbon dioxide expected is one mol of CO2 or 44 grams of CO2.
Sadly the amount you will get will probably be less than 44 grams and more like 34 grams of CO2. The problem is a competing reaction that happens. Some carbon reacts to make CO.
2 C(s) + O2(g) --- > 2 CO(g)
The carbon participating in this "side" reaction will not be able to make CO2. The reaction will not yield 100% of the expected CO2.
The amount of carbon dioxide produced, 34 grams of CO2 is only 77% and not 100 % of the expected 44 grams.
The percent yield is defined as 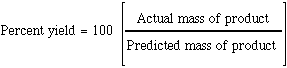 |
| The predicted yield is determined by the masses used in a reaction and the mole ratios in the balanced equation. This predicted yield is the "ideal". It is not always possible to get this amount of product. Reactions are not always simple. There often are competing reactions. For example, if you burn carbon in air you can get carbon dioxide and carbon monoxide formed. The two reactions occur simultaneously. Some carbon atoms end up in CO and others end up in CO2. The typical calculation in a starting class assumes that there is only one path for the reactants. This is an over simplification.You know for example from real life that food is not always converted to energy. If you eat a cookie, some of it could end up stored as "fat" Ugh! |
| Example: |
| What is the percent yield for a reaction if you predicted the formation of 21. grams of C6H12 and actually recovered only 3.8 grams? |
1. Recall definition of percent yield. | 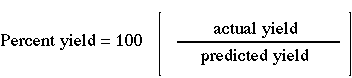 |
2. Substitute the actual and predicted yields. | 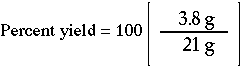 |
3. Answer: The percent yield is 18 %. |
Example 2: |
| A reaction between solid sulfur and oxygen produces sulfur dioxide. |
| The reaction started with 384 grams of S6 (s). Assume an unlimited supply of oxygen. What is the predicted yield and the percent yield if only 680 grams of sulfur dioxide are produced? |
| 1 S6 (s) | 6 O2 (g) | 6 SO2 (g) | |
 | | |       |
Step 1 : Calculate the molar masses for S6 (s) and SO2(g). The oxygen has no effect on the answer because there is more than you need. 1 mole S6 (s)= 193 grams S6 (s); 1 mole SO2(g) = 64 grams SO2(g) |
Step 2 : Mole ration method Determine the mole ratio for 1 mole S6 (s) to mole SO2(g) The balanced equation indicates 1 mole S6 (s) to 6 mole SO2(g) |
Step 3 : Calculate the number of moles of S6 (s) moles S6 (s) = [384 g S6 (s)][ 1 mole S6 (s)/ 192 g S6 (s)] = 2 moles S6 (s) |
Step 4 : Calculate the moles of SO2(g) expected using the mole ratio 6 moles SO2(g) / 1 mole S6 (s) moles SO2(g) = 2 moles S6 (s)[6 SO2(g) / 1 S6 (s)] = 12 moles SO2(g) |
Step 5 : Calculate the grams of SO2(g) predicted using 1 mole SO2(g) = 64 grams SO2(g) grams SO2(g) = 12 moles SO2(g)[64 grams SO2(g)/1 mole SO2(g)] = 768 g SO2(g) |
Step 6 : Calculate the percent yield using the definition
Percent yield = 100[actual yield/ predicted yield] = 100[680 grams SO2(g)/ 768 g SO2(g)]= 89%
Subscribe to:
Comments (Atom)
